Wielość wariantów STV wynika głównie z mnogości prób wymyślenia wersji, która, posiadając zalety STV, pozbawiona byłaby jednocześnie jak największej liczby wad, wychodzących na jaw wraz z rozpowszechnianiem się metody.
Istniejące odmiany możemy z grubsza podzielić na dwie grupy: klasyczne (zwykle pochodzące z XIX wieku, nieskomplikowane obliczeniowo) i nowoczesne (będące wynikiem refleksji teoretycznej badaczy, wymagające komputerów).
Punktem wyjścia do prezentacji różnych odmian STV niech będzie wariant poniższy, klasyczny – nazwijmy go podstawową wersją STV.
1. STV w wersji podstawowej
Jest to standardowy wariant Hare’a uzupełniony o dokładny transfer głosów:
- Po przeliczeniu głosów oblicza się kwotę Hare’a.
- Liczone są głosy na każdego z kandydatów (za głos na kandydata uznaje się głos na którym kandydat ów znajduje się najwyżej na liście preferencji. Nie uwzględnia się kandydatów już wybranych bądź odrzuconych. W pierwszym przeliczeniu będą to głosy 1. preferencji na kandydata). Jeśli liczba głosów na danego kandydata przekracza kwotę lub jest jej równa, kandydatowi przyznawany jest mandat.
- Dokonywany jest transfer głosów nadwyżkowych kandydatów, którzy uzyskali mandat. Nadwyżki transferowane są w kolejności od największej do najmniejszej. Głosy powyżej kwoty są przekazywane kandydatom następnym na liście preferencji. Jeśli właśnie wybrany kandydat był ostatni na liście, głos odrzucamy i nie bierze on udziału w dalszych obliczeniach. Przekazywanie głosów przebiega zgodnie z opisaną wcześniej procedurą transferu dokładnego (głosom przypisywane są wagi). Po transferze wybrany kandydat jest usuwany ze wszystkich głosów(kandydaci usytuowani za nim w hierarchii preferencji „awansują” w ten sposób o jeden stopień wyżej) i nie bierze dalej udziału w procedurze.
Po dokonaniu transferu(ów) ponownie przeliczamy głosy i wracamy do punktu 2. - Jeśli po którymkolwiek z przeliczeń żaden z kandydatów nie osiągnie kwoty głosów, a liczba pozostałych kandydatów przekracza liczbę pozostałych do przydzielenia miejsc mandatowych, odrzuca się kandydata o najmniejszej liczbie głosów. Wszystkie jego głosy są transferowane z wagą równą 1.
- Jeśli liczba pozostałych kandydatów jest równa liczbie pozostałych do przydzielenia miejsc mandatowych, wszyscy kandydaci są uznawani za wybranych.
- Procedura kończy się z chwilą obsadzenia wszystkich miejsc mandatowych.
| PRZYKŁAD (Preferencje wyborców w przykładach zapisywane są następująco: liczba głosów o takim szeregu preferencji, kandydat pierwszej preferencji, kandydat drugiej preferencji, …, kandydat ostatniej preferencji. Głosy na kandydatów przedstawiane są następująco: nazwa kandydata, liczba oddanych na niego głosów..) Wariant podstawowy STV. 5 kandydatów: A, B, C, D, E, 60 głosów, 3 miejsca do obsadzenia.kwota 60/3=20. | Preferencje wyborców: 15 A B C D 10 A B D C 15 B A C D 9 C D B A 8 D C B 3 E D C |
| 1. przeliczenie, głosy na kandydatów: A 25 – wybrany B 15 C 9 D 8 E 3 Transfer: 15/25 * 5 głosów → B C D 10/25 * 5 głosów → B D C |
Głosy po transferze: 15+3=18 B C D 2 B D C 9 C D B 8 D C B 3 E D C |
| 2. przeliczenie, głosy na kandydatów: B 20 – wybrany C 9 D 8 E 3 Żaden głos nie jest transferowany, bo nie ma nadwyżki. |
Głosy po transferze: 9 C D 8 D C 3 E D C |
| 3. przeliczenie, głosy na kandydatów: 9 C 8 D 3 E – skreślony Skreślamy kandydata o najmniejszej liczbie głosów, a jego głosy transferujemy. |
Głosy po transferze: 9 C D 11 D C |
| 4. przeliczenie, głosy na kandydatów: 9 C – skreślony 11 D |
Głosy po transferze: 20 D |
| 5. przeliczenie, głosy na kandydatów: 20 D – wybrany |
|
| Wybrani kandydaci: A B D. |
Zdefiniowana w ten sposób podstawowa wersja STV zapewnia odzwierciedlenie różnorodności poglądów elektoratu w zestawie wybieranych osób. Zauważmy, że w powyższym wariancie żaden głos się nie marnuje – każdy w końcu przyczynia się do wybrania jakiegoś kandydata (z wyłączeniem tych, które zawierają za mało kandydatów na liście preferencji i w pewnym momencie ‘wypadają z gry’).
2. Metoda Hare’a
Metoda Hare’a (w wersji ostatecznej – Hare kilkakrotnie modyfikował swoje rozwiązania) jest tożsama z wersją podstawową z jednym wyjątkiem: Hare proponował transfer losowy.
3. Metoda Andrae
Metoda Andrae, najwcześniejsza chronologicznie z tutaj omawianych, zawierała w sobie także transfer losowy. Co więcej, Andrae nie znał idei odrzucania kandydatów o najniższej liczbie głosów w wypadku braku dostępnych głosów do transferu, a w zamian proponował inny algorytm. Aby opisać tę metodę, należy w opisie metody podstawowej skreślić punkt 5., a 4. zmodyfikować następująco:
- Jeśli po którymkolwiek z przeliczeń żaden z kandydatów nie osiągnie kwoty głosów, a liczba pozostałych kandydatów przekracza liczbę pozostałych do przydzielenia miejsc mandatowych, mandaty przydzielamy tym kandydatom, którzy w danej chwili mają najwięcej głosów, nie mniej jednak niż połowa kwoty. Jeśli w ten sposób nie obsadzimy wszystkich miejsc, pozostałe mandaty obsadzają Ci kandydaci, którzy nie zostali dotąd wybrani, a mieli najwięcej głosów pierwszej preferencji.
| PRZYKŁAD – Metoda Andrae – dane początkowe jak w przykładzie 1. 5 kandydatów: A, B, C, D, E, 60 głosów, 3 miejsca do obsadzenia. Kwota 60/3=20. | Preferencje wyborców: 15 A B C D 10 A B D C 15 B A C D 9 C D B A 8 D C B 3 E D C |
| Pierwsze dwa przeliczenia jak w przykładzie 1 (dla uproszczenia pomińmy ewentualne zaburzenia wprowadzane przez losowość transferu). | |
| 3. przeliczenie, głosy na kandydatów: 9 C – wybrany 8 D 3 E Wybieramy kandydata o największej liczbie głosów, nie mniejszej niż połowa kwoty=10 – nie ma takiego. Wybieramy kandydata o największej liczbie głosów 1. preferencji – jest to C z 9 głosami. |
|
| Wybrani kandydaci: A B C. |
Słabość tego algorytmu uwidacznia się w momencie, gdy głosy są rozdrobnione i żaden z kandydatów nie osiąga kwoty (stosunkowo częsta sytuacja, szczególnie w dalszych przeliczeniach). Działa on wtedy jak SNTV, z całym bagażem jej wad (marnowanie głosów, konieczność głosowania strategicznego, możliwość manipulacji poprzez dołączanie nowych kandydatów, itd.). Ponadto rezygnacja z odrzucania najsłabszych kandydatów oznacza także rezygnację z wykorzystania dalszych preferencji ich wyborców. W wyniku tego okazać się może że część wybranych kandydatów popieranych było przez niewielką liczbę wyborców, co daje im słaby mandat i osłabia legitymizację całego procesu wyborczego (takim kandydatem jest C z przykładu).
4. Metoda Hare’a-Clarka
Metoda Hare’a-Clarka jest tożsama z metodą podstawową, z tym, że używa się kwoty Droopa zamiast kwoty Hare’a. Identyczny algorytm używany jest w ordynacji wyborczej do Senatu Związku Australijskiego.
5. „Reguły senatorskie”
„Reguły senatorskie” to pierwsza historycznie metoda używająca transferu dokładnego, opracowana przez Gregory’ego. Modyfikacje w stosunku do wariantu standardowego są następujące:
- Zamiast kwoty Hare’a używamy kwoty Droopa,
- Dokonując transferu, przekazujemy innym kandydatom jedynie tyle głosów, ile im ‘potrzeba’ do uzyskania kwoty (jeżeli jest to w rezultacie tego transferu możliwe). W ten sposób transferowane są głosy tylko z początkowego zestawu (nadwyżki kandydatów, którzy przekroczyli kwotę w pierwszym przeliczeniu) – ich transfer nie powoduje następnych przepływów głosów. Kolejny transfer może nastąpić tylko w wyniku odrzucenia kandydata o najmniejszej liczbie głosów.
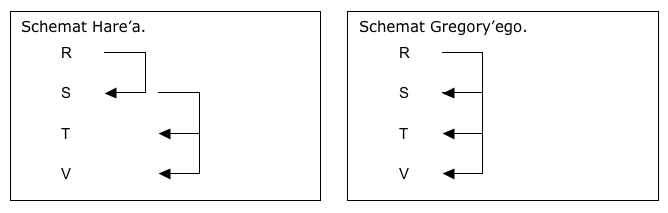
Metoda ta używa więc schematu transferu, który nazwałem schematem Gregory’ego.
W dalszym wywodzie używać będę nowego przykładu. Aby pokazać różnice w przepływie głosów między wariantem senatorskim i standardowym zastosuję kwotę Newlanda-Brittona.
| PRZYKŁAD – Reguły senatorskie z kwotą NB. 5. kandydatów: R, S, T, U, V, 80 głosów, 3 miejsca do obsadzenia. qNB=20. | Preferencje wyborców: 25 RSVUT 15 RSTUV 9 SRTUV 9 SUTRV 6 TURSV 7 UTSRV 9 VTURS |
| 1. przeliczenie: 40 R – wybrany 18 S itd. 20 gł. transferujemy w proporcjach: 25/40 SVUT 15/40 STUV Ale S potrzebuje do kwoty tylko 2 głosy. Cała więc reszta mu przysługująca (18 gł.) transferowana jest dalej. |
Głosy po transferze: 1.25 S(VUT) [nawias pokazuje, że dalszy transfer jest jedynie potencjalny] 0.75 S(TUV) 9 STUV 9 SUTV 11.25 VUT 6.75 TUV 6 TUSV 7 UTSV 9 VTUS |
| 2. przeliczenie: 20 S – wybrany 20.25 V – wybrany 12.75 T 7 U Uwaga: ortodoksyjnie wedle reguły byłoby przekazać V tyle głosów, aby uzyskał(a) on(a) dokładnie 20 głosów. Ponieważ jednak jest to ostatni kandydat, który uznany zostaje za wybranego, ta różnica nie ma znaczenia. |
|
| Wybrani kandydaci: R S V. |
Aby uchwycić różnicę w algorytmie transferu, prześledźmy ten sam przykład przy użyciu metody podstawowej:
| PRZYKŁAD – Wariant podstawowy z kwotą NB.5. kandydatów: R, S, T, U, V, 80 głosów, 3 miejsca do obsadzenia. qNB=20. | Preferencje wyborców: 25 RSVUT 15 RSTUV 9 SRTUV 9 SUTRV 6 TURSV 7 UTSRV 9 VTURS |
| 1. przeliczenie: 40 R – wybrany 18 S itd. 20 gł. transferujemy w proporcjach: 25/40 SVUT 15/40 STUV |
Głosy po transferze: 12.5 SVUT 9+7.5=16.5 STUV 9 SUTV 6 TUSV 7 UTSV 9 VTUS |
| 2. przeliczenie: 38 S – wybrany 6 T 7 U 9 V 18 głosów transferujemy w proporcjach: 12.5/38 VUT 16.5/38 TUV 9/38 UTV |
Głosy po transferze:5.9 VUT 7.8+6=13.8 TUV 4.3+7=11.3 UTV 9 VTU |
| 3. przeliczenie: 14.9 V, etc. Żaden z kandydatów nie uzyskuje kwoty, odrzucamy U, transferując jego głosy na T. |
Głosy po transferze: 14.9 VT 25.1 TV |
| 4. przeliczenie: 25.1 T – wybrany 14.9 V |
|
| Kandydaci wybrani R, S, T. |
Różnice w schematach transferu ilustruje poniższy rysunek:
6. Metoda Meeka
Metoda Meeka, oprócz innego podejścia do problemu kwoty (jest ona obliczana dla każdego przeliczenia głosów od nowa), różni się od metod klasycznych przede wszystkim systemem dokonywania transferu. Każdemu kandydatowi przypisywana jest liczba, nazywana wartością utrzymania głosów (φ, w anglosaskiej literaturze zwaną retention fraction albo keep value.). W danej chwili kandydat posiada ułamek φ z głosów, które na niego oddano i głosów, które dostał w wyniku transferu. Jego głosy natomiast transferowane są z wagą (1- φ), tak, aby suma wszystkich jego głosów pozostawała niezmienna. Wartość utrzymania każdego kandydata przy pierwszym przeliczeniu głosów wynosi jeden. Następnie po każdym przeliczeniu głosów dokonuje się ponownego obliczenia wartości utrzymania kandydatów – w ten sposób kandydaci już wybrani otrzymują wartości utrzymania mniejsze niż 1. Wartości oblicza się w ten sposób, aby każdy wybrany kandydat, po uwzględnieniu głosów własnych i otrzymanych z transferu, posiadał dokładnie jedną kwotę głosów.
Rozważmy prosty przykład:
| PRZYKŁAD – Metoda Meeka. 4 kandydaci: A B C D, 80 głosów, 3 miejsca,qNB=20. | Preferencje wyborców: 30 ABCD 25 CABD 15 BADC 10 DBCA |
| 1. przeliczenie: 30 A – wybrany 25 C – wybrany 15 B 10 D Obliczamy współczynniki: fa(30+25(1-fc))=20fc(25)=20 → fc=4/5, fa=4/7.fb=fd=1. transfer dla BCD = 30(1-fa)=12.9 transfer dla BD = 25(1-fc)(1-fa)=2.1 Suma transferowanych głosów wynosi 15. Jest to tyle ile wynosi nadwyżka ponad kwotę obu kandydatów. |
Głosy po transferze: 12.9 ABCD 2.1 CABD 15 BADC 10 DBCA (podkreślono kandydatów wybranych) |
| 2. przeliczenie: 30 B – wybrany 10 D. |
|
| Wybrani kandydaci: A C B. |
Zauważmy, że nie wykreśla się mechanicznie wybranych już kandydatów z dalszych miejsc list preferencji – pozostają oni tam, aż będzie można dokonać transferu na występującymi za nimi kandydata, który to transfer musi uwzględnić wartość utrzymania kandydata wybranego.
Aby pokazać, czym różni się w praktyce metoda Meeka od poprzednich, zastosuję ją do przykładu wykorzystywanego już wyżej dwa razy.
| PRZYKŁAD – Metoda Meeka. 5 kandydatów: R, S, T, U, V, 80 głosów, 3 miejsca do obsadzenia. qNB=20. | Preferencje wyborców: 25 RSVUT 15 RSTUV 9 SRTUV 9 SUTRV 6 TURSV 7 UTSRV 9 VTURS |
| 1. przeliczenie: 40 R – wybrany 18 S itd. fr(40)=20, fr=1/2. ½*40 gł. transferujemy w proporcjach: 25/40 SVUT 15/40 STUV |
Głosy po transferze: 12.5 RSVUT 7.5R STUV 9 SRTUV 9 SUTRV 6 TURSV 7 UTSRV 9 VTURS |
| 2. przeliczenie: 38 S – wybrany 6 T 7 U 9 V fr(40+9(1-fs))=20 (po wykluczeniu S, 9 głosów z odpowiednią wartością utrzymania przejdzie do R) fs(18+40(1-fr))=20fr=0.45, fs=0.5 transfer: VUT 25(1-fr)(1-fs) =6.88 TUV 15(1-fr)(1-fs)=4.13, itd. |
Głosy po transferze: 6.88 RSVUT 4.13 RSTUV 2.48 SRTUV 4.5 SUTRV 6 TURSV 7 UTSRV 9 VTURS |
| 3. przeliczenie: 15.88 V, etc. Żaden z kandydatów nie uzyskuje kwoty, odrzucamy U, transferując jego głosy na T. Możemy bezpiecznie wykreślić U ze wszystkich głosów – jego wartość utrzymania zostaje ustawiona na 0. |
Głosy po transferze: 6.88 RSVT 4.13 RSTV 2.48 SRTV 4.5 STRV 6 TRSV 7 TSRV 9 VTRS |
| 4. przeliczenie 24.1 T – wybrany |
|
| Kandydaci wybrani R, S, T. |
Analiza powyższego przykładu prowadzi do następującego diagramu przepływu głosów:
7. Metoda Warrena
Metoda Warrena jest modyfikacją metody Meeka, dokonaną przez C. H. E. Warrena. Argumentuje on, iż niewłaściwym jest obciążanie wyborców różnymi kosztami wyboru tego samego kandydata, w zależności od jego pozycji na ich rankingach. Zauważa on, że (w przykładzie 6) koszt wyboru S dla wyborców, których karty zaczynają się od RS, wynosi 0.28. Jest to zdecydowanie mniej, niż koszt wyboru tego samego kandydata przez wyborców, którzy zaznaczyli S jako swą pierwszą preferencję (0.5). Warren proponuje, aby wszystkie głosy oddane na jednego z wybranych kandydatów kosztowały tyle samo, bez względu na to, na jakiej pozycji na liście preferencji się on znajduje. W wypadku poprzedniego przykładu, prowadzi to do następujących obciążeń na drugim etapie przeliczania: każdy głosujący na R obciążany jest kosztem wynoszącym 20/49 (tj. ilorazem kwoty i całkowitej liczby wyborców głosujących na R w tym etapie), podobnie wyborcy S ‘oddają’ 20/58 swych głosów na S (reszta, tj. 1-20/58, podlega transferowi). Wynika z tego, że głosy RSVUT transferowane są na rzecz V z wagą wynoszącą 1-(20/49)-(20/58)=0.25, itd. Daje się zauważyć, że mimo, iż różnice między wagami wynikającymi z metod Meeka i Warrena nie są duże, to mogą przynosić różnice w wyniku. W naszym przykładzie metoda Warrena wskazuje na R, S i U jako zwycięzców (Metoda Meeka wybierała T zamiast U).
8. Inne metody zbliżone do STV
Wady klasycznych wersji STV (możliwość nie wybrania zwycięzcy Condorceta, negatywna reaktywność – więcej tutaj) biorą się w dużej mierze z sekwencyjnej eliminacji kandydatów o najmniejszej liczbie głosów. Wynik procedury zależy od kolejności tej eliminacji, a ta może być dosyć przypadkowa przy zbliżonej liczbie głosów. Istnieje więc szereg metod, które rezygnują ze standardowej metody transferowania głosów od najsłabszych kandydatów. Trudno je nazwać odmianami STV – jest to bardziej luźna wariacja na temat.
STV z porównywaniem parami (CPO-STV, Comparison of Pairs of Outcomes by the STV, STV by Paired Comparisons), wariant opracowany przez Nicolausa Tidemana, został zaprojektowany w taki sposób, że jeśli w głosowaniu istnieje zwycięzca Condorceta, to zawsze otrzyma mandat. Zamiast odrzucania najsłabszych kandydatów patrzymy na wszystkie potencjalne rezultaty (czyli listy kandydatów, którzy otrzymają mandat – liczba kandydatów na każdej takiej liście jest zawsze równa liczbie mandatów do obsadzenia w wyborach) i porównujemy je ze sobą (każda z każdą). Robi się to w kilku krokach:
- odrzucamy wszystkich kandydatów, których nie ma na obu porównywanych listach,
- liczymy głosy wewnątrz każdej listy,
- jeśli jakiś kandydat przekroczył kwotę i jest on na obu listach, jego nadwyżkę transferujemy; jeśli jest tylko na jednej liście, nadwyżka nie jest przekazywana
Po przekazaniu wszystkich nadwyżek liczymy sumę głosów na kandydatów z każdej z list. Ta lista, której kandydaci dostali sumarycznie więcej głosów, zwycięża. Jeśli znajdziemy listę, która wygrywa w ten sposób ze wszystkimi pozostałymi (listę Condorceta), wtedy mamy wynik – wszyscy kandydaci na tej liście dostają mandat. Tak jednak nie musi być – może się zdarzyć, że wszystkie listy zaliczyły i wygrane i porażki w starciu z innymi. Wtedy musimy zastosować jakieś inne kryterium – np. maksyminu, tzn. taką regułę, która każe wybrać tę listę, której najgorsza przegrana w starciu z którąkolwiek inną jest najmniejsza w porównaniu z najgorszymi przegranymi wszystkich innych list.
Metoda przekazywania transferów jest dowolna, w celu uzyskania dobrych właściwości metody warto stosować transferowanie Meeka albo Warrena.
Przy dużej liczbie kandydatów i mandatów do obsadzenia liczba porównań jest olbrzymia – wymaga to sporej mocy obliczeniowej. Cała procedura przeliczania głosów jest dosyć nieprzejrzysta – trudno się spodziewać, aby można było sprawdzić jej poprawność ręcznie, jeśli liczba porównań list może sięgać setek tysięcy. Ma jednak niewątpliwie mniej wad niż tradycyjne STV.
Istnieją także inne propozycje: metoda Dummetta skupia się na poszukiwaniu silnych koalicji zwartych i przyznawaniu miejsc mandatowych kandydatom przez nie popieranym. STV korzystająca z algorytmu Schulzego (Schulze STV) natomiast minimalizuje niektóre możliwości głosowania strategicznego. Korzysta się w niej z porównań parami (tak jak powyżej w wariancie CPO-STV) i oraz poszukiwania najsilniejszej ścieżki (w sensie Schulzego).
Dalej: Właściwości STV